Conduct and Interpret a (Pearson) Bivariate Correlation
What is a Bivariate (Pearson) Correlation?
Statisticians widely use the term Bivariate Correlation. In fact, people introduced it into the English language in 1561, 200 years before most of the modern statistic tests were discovered. It derives from the Latin word correlation, which means relation. Correlation generally describes how two or more phenomena occur together and are therefore linked. Many academic questions and theories investigate these relationships. Is the time and intensity of exposure to sunlight related the likelihood of getting skin cancer? Are people more likely to repeat a visit to a museum the more satisfied they are? Do older people earn more money? Does inflation influence wages? Do higher oil prices increase the cost of shipping? It is very important, however, to stress that correlation does not imply causation.
A correlation expresses the strength of linkage or co-occurrence between two variables in a single value between -1 and +1. We call this value that measures the strength of linkage the correlation coefficient, typically as the letter r.
We also call the correlation coefficient between two continuous-level variables the Pearson’s r or Pearson product-moment correlation coefficient. A positive r value expresses a positive relationship between the two variables (the larger A, the larger B) while a negative r value indicates a negative relationship (the larger A, the smaller B). A correlation coefficient of zero indicates no relationship between the variables at all. However, correlations only show linear relationships between variables. Even if the correlation coefficient is zero, a non-linear relationship might exist.
Bivariate (Pearson) Correlation in SPSS
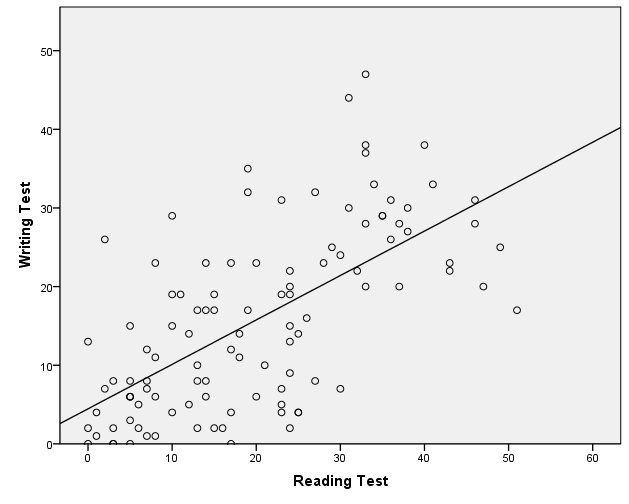
At this point it would be beneficial to create a scatter plot to visualize the relationship between our two test scores in reading and writing. The purpose of the scatter plot is to verify that the variables have a linear relationship. Other forms of relationship (circle, square) are not detected by Pearson’s Correlation Analysis. This would create a type II error because it would not reject the null hypothesis of the test of independence (‘the two variables are independent and not correlated in the universe’) although the variables are in reality dependent, just not linearly.
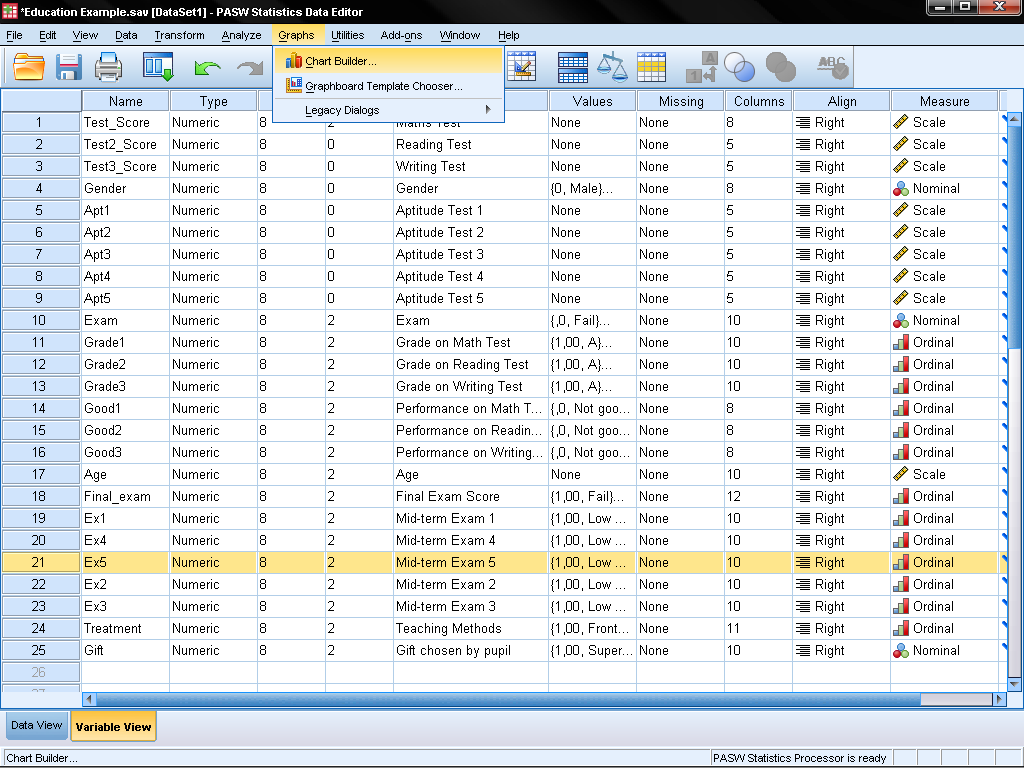
You can find the scatter plot either in Graphs/Chart Builder… or in Graphs/Legacy Dialog/Scatter Dot…
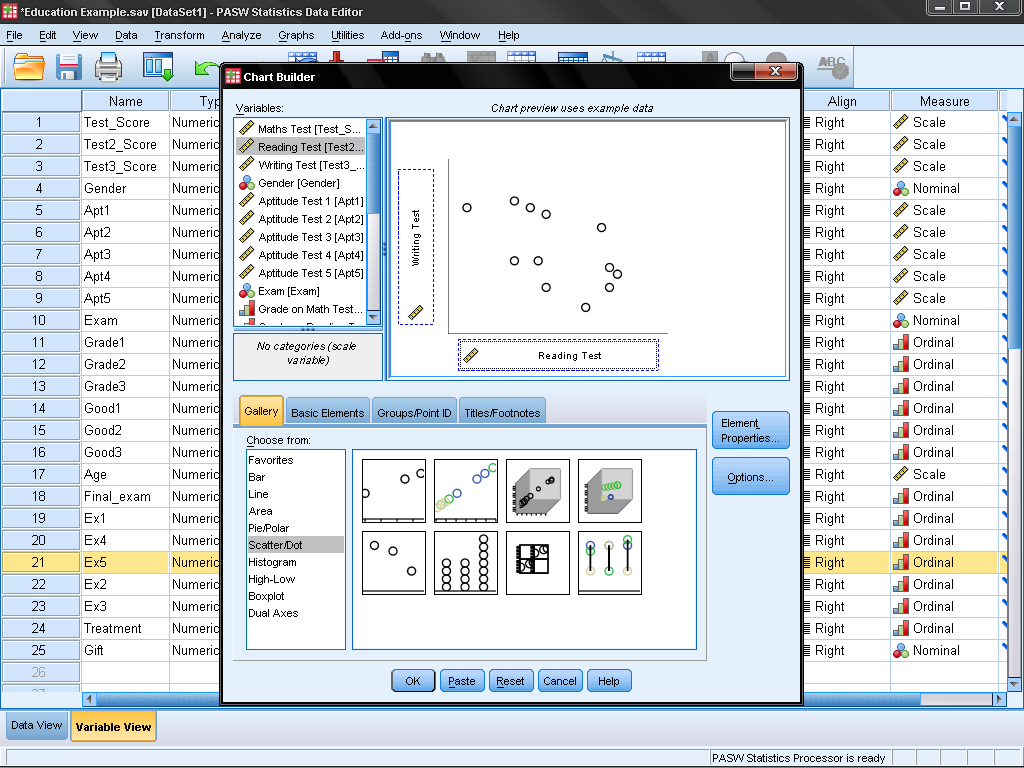
In the Chart Builder we simply choose in the Gallery tab the Scatter/Dotgroup of charts and drag the ‘Simple Scatter’ diagram (the first one) on the chart canvas. Next we drag variable Test_Score on the y-axis and variable Test2_Score on the x-Axis.
SPSS generates the scatter plot for the two variables. Double click on the output diagram to open the chart editor and click on ‘Add Fit Line’ to add a linearly fitted line that represents the linear association shown by Pearson’s bivariate correlation.
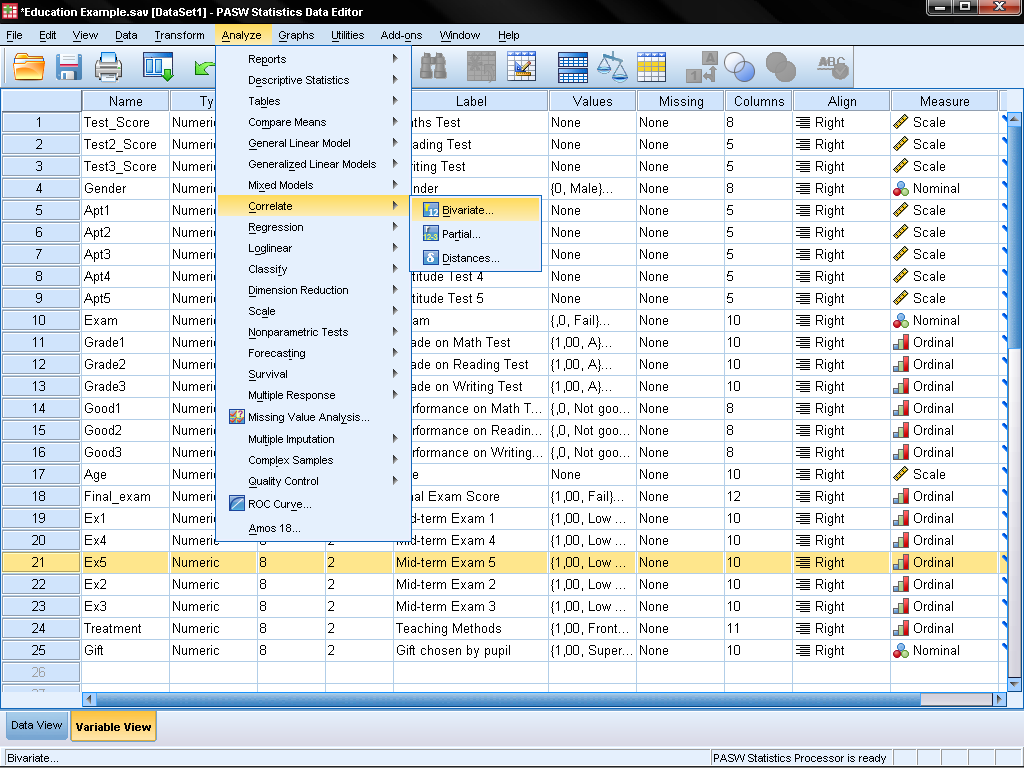
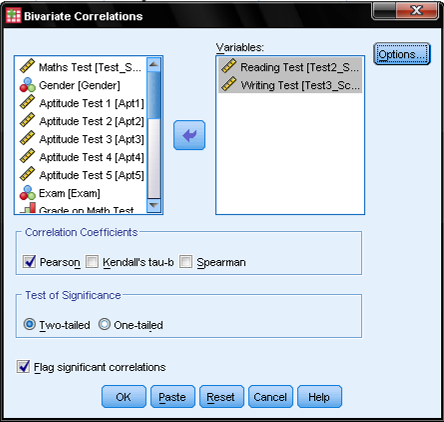
To calculate Pearson’s bivariate correlation coefficient in SPSS we have to open the dialog in Analyze/Correlation/Bivariate…
This opens the dialog box for all bivariate correlations (Pearson’s, Kendall’s, Spearman). Simply select the variables you want to calculate the bivariate correlation for and add them with the arrow.
Select the bivariate correlation coefficient you need, in this case Pearson’s. For the Test of Significance we select the two-tailed test of significance, because we do not have an assumption whether it is a positive or negative correlation between the two variables Reading and Writing. We also leave the default tick mark at flag significant correlations which will add a little asterisk to all correlation coefficients with p<0.05 in the SPSS output.
Additional Resources
We find Output, syntax, and interpretation in our downloadable manual: Statistical Analysis: A Manual on Dissertation Statistics in SPSS (included in our member resources). Click here to download.
A correlation expresses the strength of linkage or co-occurrence between to variables in a single value between -1 and +1. We call the value that measures the strength of linkage the correlation coefficient, typically represented as the letter r.
People also call the correlation coefficient between two continuous-level variables the Pearson’s r or Pearson product-moment correlation coefficient. A positive r value expresses a positive relationship between the two variables (the larger A, the larger B) while a negative r value indicates a negative relationship (the larger A, the smaller B). A correlation coefficient of zero indicates no relationship between the variables at all. However, correlations only show linear relationships between variables. Even if the correlation coefficient is zero, a non-linear relationship might exist.