Assumptions of Multiple Linear Regression Analysis
Multiple linear regression analysis is predicated on several fundamental assumptions that ensure the validity and reliability of its results. Understanding and verifying these assumptions is crucial for accurate model interpretation and prediction.
Linear Relationship
- The core premise of multiple linear regression is the existence of a linear relationship between the dependent (outcome) variable and the independent variables. This linearity can be visually inspected using scatterplots, which should reveal a straight-line relationship rather than a curvilinear one.
- Multivariate Normality: The analysis assumes that the residuals (the differences between observed and predicted values) are normally distributed. This assumption can be assessed by examining histograms or Q-Q plots of the residuals, or through statistical tests such as the Kolmogorov-Smirnov test.
- No Multicollinearity: It is essential that the independent variables are not too highly correlated with each other, a condition known as multicollinearity. This can be checked using:
- Correlation matrices, where correlation coefficients should ideally be below 0.80.
- Variance Inflation Factor (VIF), with VIF values above 10 indicating problematic multicollinearity. Solutions may include centering the data (subtracting the mean score from each observation) or removing the variables causing multicollinearity.
- Homoscedasticity: The variance of error terms (residuals) should be consistent across all levels of the independent variables. A scatterplot of residuals versus predicted values should not display any discernible pattern, such as a cone-shaped distribution, which would indicate heteroscedasticity. Addressing heteroscedasticity might involve data transformation or adding a quadratic term to the model.
Sample Size and Variable Types:
The model requires at least two independent variables, which can be of nominal, ordinal, or interval/ratio scale. A general guideline for sample size is a minimum of 20 cases per independent variable.
Assumptions of Linear Regression: Linearity, Normality, and Multicollinearity:
First, linear regression needs the relationship between the independent and dependent variables to be linear. It is also important to check for outliers since linear regression is sensitive to outlier effects. The linearity assumption can best be tested with scatter plots, the following two examples depict two cases, where no and little linearity is present.
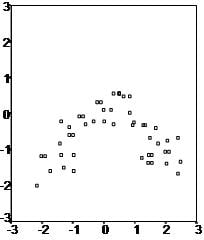
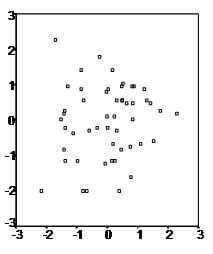
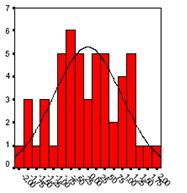
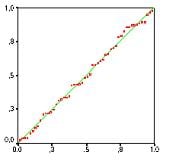
Secondly, the linear regression analysis requires all variables to be multivariate normal. One can best check this assumption with a histogram or a Q-Q plot. The individual can check normality using a goodness-of-fit test, such as the Kolmogorov-Smirnov test. If the data does not follow the normal distribution, a non-linear transformation (e.g., log-transformation) can fix the issue.
Thirdly, linear regression assumes that there is little or no multicollinearity in the data. Multicollinearity occurs when the independent variables highly correlate with each other.
Testing for Multicollinearity in Linear Regression
The following three central criteria may test the Multicollinearity:
1) Correlation matrix
When computing the matrix of Pearson’s Bivariate Correlation among all independent variables the correlation coefficients need to be smaller than 1.
2) Tolerance
The tolerance measures the influence of one independent variable on all other independent variables; one can calculate it with an initial linear regression analysis. Tolerance is defined as T = 1 – R² for these first step regression analysis. With T < 0.1 there might be multicollinearity in the data and with T < 0.01 there certainly is.
3) Variance Inflation Factor (VIF)
VIF = 1/T is the term of the variance inflation factor of the linear regression. With VIF > 5 there is an indication that multicollinearity may be present; with VIF > 10 there is certainly multicollinearity among the variables.
If you find multicollinearity in the data, centering the data (i.e., subtracting the mean of the variable from each score) can help solve the problem. However, the simplest way to address the problem is to remove independent variables with high VIF values.
Fourth, linear regression analysis requires that there is little or no autocorrelation in the data. Autocorrelation occurs when the residuals are not independent from each other. For instance, this typically occurs in stock prices, where the price is not independent from the previous price.
4) Condition Index
The factor analysis on the independent variables calculates the condition index. Values of 10-30 indicate a mediocre multicollinearity in the linear regression variables, values > 30 indicate strong multicollinearity.
Addressing multicollinearity
If multicollinearity finds in the data centering the data, i.e. deducting the mean score might help to solve the problem. Other alternatives to tackle the problems is conducting a factor analysis and rotating the factors to insure independence of the factors in the linear regression analysis.
Fourthly, linear regression analysis requires that there is little or no autocorrelation in the data. Autocorrelation occurs when the residuals are not independent from each other. In other words when the value of y(x+1) is not independent from the value of y(x).
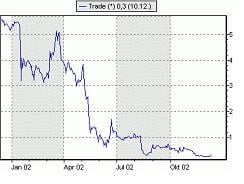
Understanding Autocorrelation in Linear Regression
While a scatterplot allows you to check for autocorrelations, you can test the linear regression model for autocorrelation with the Durbin-Watson test. Durbin-Watson’s d tests the null hypothesis that the residuals do not exhibit linear autocorrelation. While d can assume values between 0 and 4, values around 2 indicate no autocorrelation. As a rule of thumb values of 1.5 < d < 2.5 show that there is no auto-correlation in the data. However, the Durbin-Watson test only analyses linear autocorrelation and only between direct neighbors, which are first order effects.
The last assumption of the linear regression analysis is homoscedasticity. The scatter plot is good way to check whether the data are homoscedastic (meaning the residuals are equal across the regression line). The following scatter plots show examples of data that are not homoscedastic (i.e., heteroscedastic):
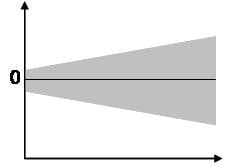
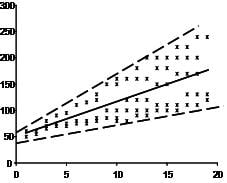
The Goldfeld-Quandt Test can help to test for heteroscedasticity. The test splits the data into two groups and tests to see if the variances of the residuals are similar across the groups. If homoscedasticity is present, a non-linear correction might fix the problem.
Related Pages:

If you’re like others, you’ve invested a lot of time and money developing your dissertation or project research. Finish strong by learning how our dissertation specialists support your efforts to cross the finish line.
