Conduct and Interpret a Profile Analysis
What is the Profile Analysis?
Profile Analysis is mainly concerned with test scores, more specifically with profiles of test scores. Why is that relevant? Researchers commonly administer tests in medicine, psychology, and education to rank study participants. A profile shows differences in scores on the test. If a psychologist administers a personality test (e.g., NEO), the respondent gets a test profile in return showing the scores on the Neuroticism, Extraversion, Agreeableness, Consciousness, and Openness dimensions. Similarly, many tests such as GMAT, GRE, SAT, and various intelligence questionnaires report profiles for abilities in reading, writing, calculating, and critically reasoning.
Researchers typically use test scores to predict behavioral outcomes. In education studies it is common to predict test performance, for example using the SAT to predict the college GPA when graduating. They widely use cluster analysis and the Q-test to build predictive models for this purpose.
What is the purpose of Profile Analysis?
Profile Analysis helps researchers to identify whether two or more groups of test takers show up as a significantly distinct profile. It helps to analyze patterns of tests, subtests, or scores. The analysis may be across groups or across scores for one individual.
What does that mean?
Profile analysis looks at profile graphs. A profile graph shows the mean score of one group of test takers compared to another group across all items. The main purpose is to assess how good a test is. Researchers administer tests with multiple item measurements over time. You could use a simple ANOVA to compare test items, but it violates the independence assumption in two key ways.
Firstly, the scores on each item are not independent because researchers design item batteries to have a high correlation. Secondly, if a test predicts group membership (e.g., depressed vs. not depressed), the item battery should best predict the outcome. Thus, the item battery and group membership are also not independent.
What is the solution to this problem?
Since item measurements and group membership are not independent, they must be treated as a paired sample. Statistically, Profile Analysis is similar to repeated measures ANOVA.
Example:
A research team wants to create a new test for a form of cancer. This test appears in patients with a specific history and diet. They collect data from ten questions answered by cancer patients and a randomly drawn sample of people without the cancer.
Profile analysis checks whether the ten questions significantly differentiate between the groups with and without the illness. It accounts for the non-random nature of item correlations and group assignments.
Profile analysis is also useful for understanding and exploring complex data. Its results help identify key differences. They use them to choose contrasts, post hoc analyses, and statistical tests when ANOVA or t-test aren’t enough. However, profile analysis has limitations, particularly regarding the standard error of measurement and predicting a single person’s score.
Alternatives to Profile Analysis include Multidimensional Scaling and Q-Analysis. In Q-Analysis, an individual’s scores on the item battery form an independent block, like in Profile Analysis. It then applies rotated factor analysis to extract factors and flag defining items.
Another alternative to Profile Analysis is a two-way MANOVA (or doubly MANOVA). This design treats repeated measures as a second dependent variable, avoiding the sphericity assumption.
The Profile Analysis in SPSS
The research question we will examine for the Profile Analysis is as follows:
Do the students who passed the final exam and the students who failed the final exam have a significantly different ranking in their math, reading, and writing test?
The Profile Analysis uses the repeated measures GLM module of SPSS, like the repeated measures ANOVA and ANCOVA. The Profile Analysis can be found in SPSS in the menu Analyze/General Linear Model/Repeated Measures…
The dialog box that opens is different than the GLM module for independent measures. Before specifying the model we need to group the repeated measures—the item battery we want to test. In our example we want to test if the standardized test, which consists of three items (math, reading, writing), correctly classifies the two groups of students that either pass or fail the final exam.
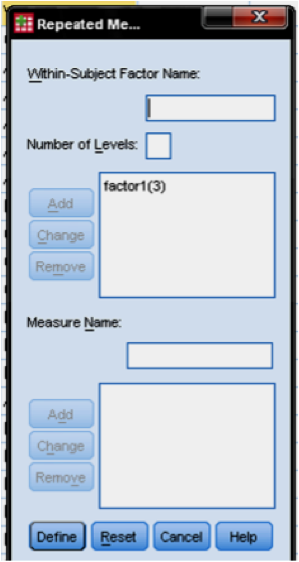
This is done by creating a within-subject factor. The item battery is the within-subject factor in Profile Analysis because it represents the different observations of one subject. Our item battery contains three items – one score for math, one for reading, and one for writing. Thus we create and add a factor labeled factor1 with three factor levels.
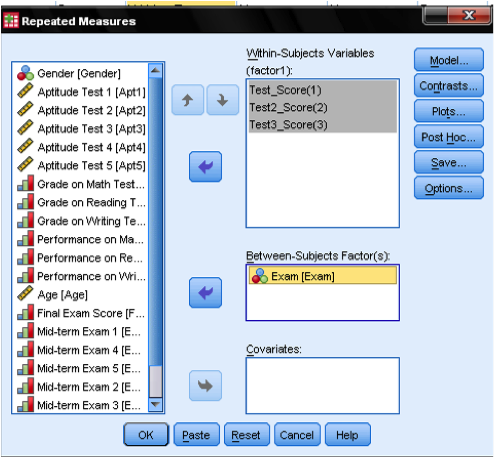
The next dialog box allows us to specify the Profile Analysis. First we need to add the three test items to the list of within-subjects variables. We then add the exam variable to the list of between-subjects factors. We can leave all other settings on default, apart from the plots.
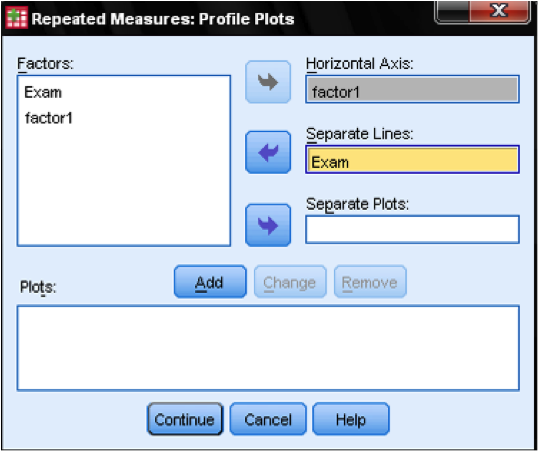
To create the profile plots we want the items (or subtests) on the horizontal axis with the groups as separate lines. We also need the Levene test for homoscedasticity to check the assumptions of the Profile Analysis, the Levene Test can be included in the dialog Options…