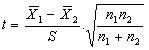Independent Sample T-Test

Quantitative Results
Statistical Analysis

The independent samples t-test analyzes the mean comparison of two independent groups. When we take two samples from the same population, then the mean of the two samples may be identical. However, when samples come from different populations, their means may differ. In this case, it helps determine whether the population means are similar or different.

Assumptions:

1. It assumes the dependent variable follows a normal distribution.
2. Assumes that the variance of the two groups are the same as the dependent variable.
3. Assumes that the two samples are independent of each other.
4. It draws samples randomly from the population.
5. All observations must be independent of each other.
6. Dependent variables must be measured on an interval or ratio scale.

Procedure:

1. Set up the hypothesis.
a. Null Hypothesis: It is assumed when the means of the two groups are not significantly different.
b. Alternative Hypothesis: Assumes that the means of the two groups are significantly different.

2. Calculate the standard deviation by using this formula:





3. Calculate the value of the independent sample t-test by using this formula:

4. Degree of freedom:
Where
V= degree of freedom
N1+N2= number of observations in both samples.

5. Hypothesis testing: Statistical decisions are made about whether or not the two population means are identical. Compare the calculated value with the table value. If the calculated value is greater than the table value of the predetermined significance level, we will reject the null hypothesis and say that the means of the two groups are different. If the calculated value of the is less than the table value, then we will say that the means of the two groups are the same.

SPSS:

1. Click on the “SPSS 16” icon from the start menu.
2. Click on the “open data” icon and select the data.
3. Click on the “analysis” option and select “compare mean” from the analysis option.
4. Select “independent sample t-test” from the compare mean option, the following window will appear:
Select the grouping variable and insert it into the grouping variable box. Define the group in the independent samples t-test. Select the dependent variable and insert them into the test variable list. Click on “option” and select “% confidence interval.” As we click on the “ok” button, the result window for the independent sample t-test will appear in front of us.
Group statistics table: This table will show the total number in each group, the mean, the standard deviation and the standard error.
Independent sample t-test statistics table: In this table, the first test will be Levene’s test, which is used to test the assumptions of equal variance between all the groups in the independent sample t-test. Significance value of F is used to make the statistical decision about the assumptions of equal variance. The second test statistics will show the calculated value of the independent sample t-test, the degree of freedom, and the significance value of the independent sample t-test. This significance value is used to make the statistical decision about the mean of the two groups. If the calculated value is less than the predetermined significance level, then we can say that the means are significantly different.
 
 
Share
Two women looking at statistics paper work
Step Boldly to Completing your Research

If you’re like others, you’ve invested a lot of time and money developing your dissertation or project research.  Finish strong by learning how our dissertation specialists support your efforts to cross the finish line.
Learn More