Sample Size Calculation
Sample size calculation is very important in statistical inference and findings. A sample is a subset of the population. It is through samples that researchers are able to draw specific conclusions regarding the population. Sample size is the size of that sample. Sample size is very important in statistics.
Statistics Solutions can assist in choosing the correct sample size for your dissertation, thesis or research. Use the calendar below to schedule a free 30-minute consultation.
Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
Sample size calculation ascertains the correct sample size that would represent the population as a whole. A larger sample size is required while making decisions when more information is needed. As the sample size increases, the information obtained has to be obtained with precision. The degree of precision may be measured in terms of the standard deviation of the mean. The standard deviation is inversely proportional to the square root of the sample size.
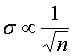
Determining Sample size:
There are many ways to determine the sample size. Sample size calculation for different statistical testing varies depending on the formulae used. Sample size calculation cannot be performed with only one method or technique.
Sample size calculation is legitimate for most relevant tests, like the t test, z test, f test, etc. To show this in an example, let us take an example of hypothesis testing.
Let us assume that Xi (i=1, 2, …n), where ‘n’ is the independent number of observations drawn from N (µ,σ2).
Here, H0: µ= 12 X’> i.e. there is no significant difference in the mean of the sample drawn from the population.
H1: µ= µ*, for some ‘smallest significant difference’ μ* >0.
While observing some significant differences, the smallest value can be considered.
To estimate our hypothesis, we must do as follows:
Zα = √n ( 12X-µ) / σ’> . Here, Zα is the value of standard normal distribution at α level of significance.
If the tabulated value of Zα > calculated value of Zα , then we accept H0 at α level of significance. Otherwise we reject it.
In order to determine the value of ‘n,’ we have the following formula:
n= (Zα σ)2 / ( 12X-µ)’> 2
Sample size calculation depends on the different statistical tests that are to be carried out, because with a change in statistical tests, the results are also dissimilar. Depending on the size of the population or the accuracy of the result, the size of the sample in sample size calculation varies.
Sample size calculation depends on many factors that are more commonly known as qualitative factors. These are important to help calculate any kind of sample size calculation and determination. These factors are the importance of decision, the resource Constraints, the number of variables, the sample sizes used in similar studies, the nature of the research, and the nature of the analysis.
In qualitative research, the sample size in sample size calculation is usually small. Larger samples would be required for conclusive research, such as descriptive surveys. Again, if the data collected is on a large number of variables, then the samples should also be large.
In market research, sample size is used for problem solving research, problem identification research, TV, radio, print advertising, test-market audits, focus groups, etc.